求解具有规定测地曲率曲线的高效几何方法

缑建杰，张 鹏，杨 扬，陈代鑫

（1.成都飞机工业（集团）有限责任公司检验检测部，四川 成都 610091 2.长沙理工大学汽车与机械工程学院，湖南 长沙 410114）

曲面上的曲线在曲面裁剪[2]、曲面过渡[2]、数控加工刀具路径规划[3]等众多应用中发挥着重要的作用。在一些应用场景中，需要设计出的曲线上测地曲率满足一定的要求，这种曲线被称为具有规定测地曲率的曲线。

例如，在自动铺带工艺中，铺放路径上测地曲率的大小直接决定了复合材料预浸带的面内变形[4]。由于预浸带面内变形能力很小，因此带料通常沿着模具曲面上的测地线铺放[5]。

测地线是具有规定测地曲率曲线中的一个特例，其上各处测地曲率均为零。自动铺带轨迹规划中经常要处理测地线求解的初值问题，即给出铺放起始点位置以及初始铺放方向，求解曲面上的唯一一条测地线。

到目前为止，该问题已经有很多经典的求解方法，具体可分为数值解法[6-7]、离散解法[8-9]以及几何解法[10-11]。

相较于测地线，本研究主要关注参数曲面上测地曲率不为零的曲线，这类曲线在图案设计、齿轮设计、机械结构设计等场合均有所应用。

文献[12]提出了一种保测地曲率的曲面曲线设计方法，其目的是在光滑曲面上进行图案设计。

在该项研究中，所需的曲面图案首先被构造为一平面图案。在曲面上指定起始点和方向后，该平面图案被逐段映射到目标曲面上。

映射过程中，为保证视觉效果，要求曲面曲线的测地曲率与平面曲线的曲率相等。

文献[13]基于保测地曲率的曲线设计方法对非圆锥齿轮传动进行了设计与分析，利用球面上具有规定测地曲率的曲线生成了非圆锥齿轮的空间三维齿廓。

文献[14]则基于球面上具有规定测地曲率的曲线设计了一种不等速行星轮系分插机构。

具有规定测地曲率的曲线也常应用于复合材料自动化加工领域中。

文献[15]提出了一种针对圆锥面模具的自动铺丝轨迹规划方法，利用等测地曲率曲线实现了纤维变形与纤维方向之间的平衡。

该方法所依据的几何学原理是可展曲面上的等测地曲率曲线实际上是其对应展开面上的一段圆弧。

文献[16]给出了一种针对自由曲面模具的自动铺带轨迹规划方法，利用具有微小测地曲率的曲线实现了预浸带在模具曲面上的转向，消除了相邻带料间过大的铺放间隙。

本研究提供一种参数曲面上具有规定测地曲率曲线的求解方法，当给出目标曲面上的起始点、方向以及测地曲率的分布时，可追踪出符合设计要求的空间曲线。

其主要由以下几个部分组成：第二节对现有的计算方法进行了分析；
第三节详细介绍了提出方法的原理；
第四节将所提出的方法与现有的方法在计算效率上进行了比较；
第五节展示了本方法的两种应用场景；
第六节则进行总结并给出结论。

在设计制造的一些应用场景中，需要设计出的曲面曲线上测地曲率满足一定的要求，并且测地曲率大小不为零。然而，现有的研究主要处理测地线的计算问题，其中多数方法无法直接用于构造具有非零测地曲率的曲线，例如数值解法以及离散解法这两类。

到目前为止，具有非零测地曲率曲线的计算方法主要可分为数值解法、分析解法以及几何解法这三类。

文献[16]基于微分几何建立了具有规定测地曲率曲线的数学模型，该数学模型由一个微分方程组表达，需要利用数值积分器进行求解。

其中曲线的设计精度与数值积分器的阶数直接相关。文献[15]提出的分析解法可以构造出准确的目标曲线，然而该方法只适用于可展曲面，应用范围较窄。

文献[12]提出的几何解法在每一步计算中需要将点投影回曲面，降低了计算效率。

文献[11]提出了一种构造测地线的几何方法，经过调整，该方法可用于求解具有非零测地曲率的曲线。该方法则直接在参数空间中进行计算，无需额外的投影操作。

现有的几何方法主要基于伏雷内公式与泰勒展开设计目标曲线。设Q(s)—目标曲线上一点，Q"(s)—曲线在该点的延伸方向，Q""(s)—曲线在该点的曲率。根据现有的几何方法可知，Q(s)在目标曲线上临近点的位置以及方向可表达为：

式中：h—计算步长。

在得到临近点位置及延伸方向后，可采用公式追踪其它离散点从而得到整段曲线。

需要注意的是，文献[12]中提出几何方法是在三维空间中追踪曲线，而文献[11]中的几何方法则在参数空间中追踪曲线。

由方程可知，现有的几何方法可以保证二阶位置计算精度与一阶方向计算精度。

设延伸方向Q"(s)计算误差为Ah2，其中A—常数。若忽略曲率Q""(s)的计算误差，则位置计算误差主要来源于以下两个部分：

（1）由于方向计算误差引起的误差：

（2）泰勒展开的余项：

显然，在每一步计算中，由于方向计算误差引起的误差ε1相对于泰勒展开的余项ε2不能忽略。

因此，现有的几何方法虽然具有二阶位置计算精度，但计算过程中由于方向计算误差引起的误差ε1不断累积，降低了最终精度。

由前述分析可知，若想获得较好的曲线设计精度，需保证方向计算精度为高阶，而这正是现有的几何方法难以保证的，其主要原因在于这些方法难以得到比曲率Q""(s)更高阶的几何信息。

对现有的规定测地曲率曲线计算方法的主要特点进行了总结与展示，如表1所示。

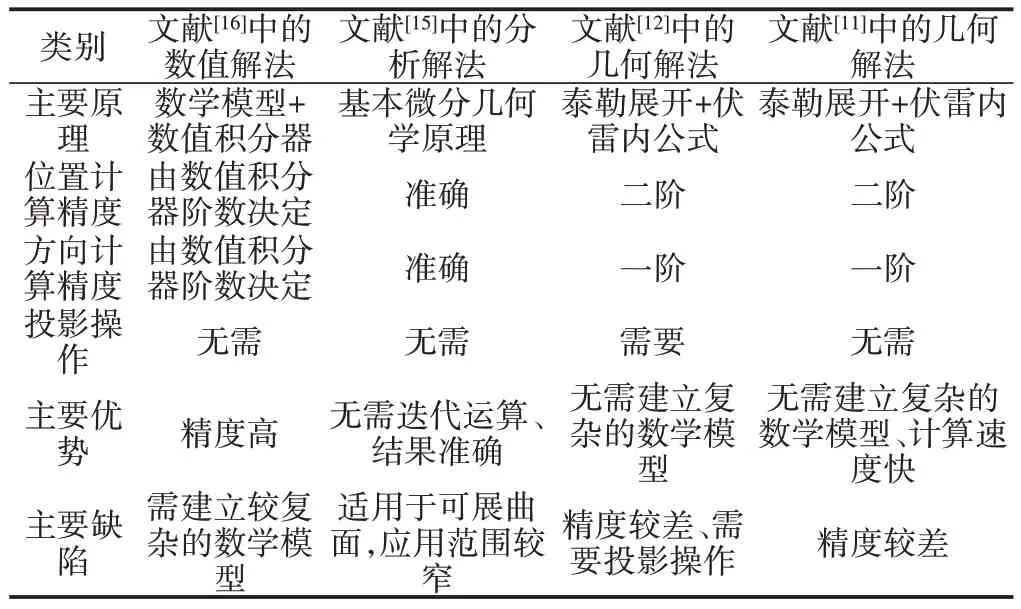
表1 现有计算方法的主要特点Tab.1 Main Features of Existing Methods

本小节介绍文中所提出方法的数学原理。设r(u，v)=[x(u，v)，y(u，v)，z(u，v)]为模具曲面S的参数方程，其中x、y、z是参数u和v的可微函数。

令C是曲面S上一条具有规定测地曲率的弧长参数化曲线，如图1所示。

图1 测地曲率与法曲率的定义Fig.1 Definition of Geodesic Curvature and Normal Curvature

图中：P—曲线C上任意一点；
N—曲面S在点P的单位法向量；
t—曲线C在P点的单位切向量。它可以用如下方程描述：

式中：s—弧长参数。

令b=N×t，则N，t，b三者彼此正交并构成一个右手坐标系。根据微分几何，曲线C在P点处的曲率向量k可表示为：

式中：kn—法曲率向量；

kg—测地曲率向量；

kn—曲面S在P点处沿切向量t的法曲率；

kg—曲线C在P点处的测地曲率。

由公式可知，曲线C在P点处的测地曲率kg可通过如下公式求解：

设P0为曲线C的初始点；

C"与P0"为曲线C与点P0在参数空间中的逆映射。

根据微分几何，曲线C"在P0"处的延伸方向l0=与曲线C在P0处的单位切向量t0之间的关系可通过下式表达：

在方程左右两侧同时点乘列向量[ru(P0")rv(P0")]T得到：

3.1 构建求解位置与方向信息的F算子

令P0为曲面上的正则点，则由公式可得，已知曲线C在三维空间中的单位切向量t0，可以求得C"在参数空间中的延伸方向l0为：

式中：E(P0")，F(P0")，G(P0")—曲面在P0"处的第一类基本量。

由点P0"位置以及延伸方向l0，可以通过一阶线性逼近得到P0"临近点P1"的位置：

在获得P1"的位置之后，为保证追踪过程能够持续进行，需计算曲线C在P1处的单位切向量t1以及C"在P1"处的延伸方向l1。由公式可知，单位切向量t0在P0点相对弧长的变化率可表达为：

在得到单位切向量t1后，可以利用与类似的公式计算l1。

显然，通过以上步骤获得的P1"与t1只具有一阶精度，在多数场合中直接应用会有较大的计算误差。为提高计算精度，首先将前述具有一阶精度的计算过程整体封装为一个F算子：

如上式所示，F算子输入为C"上某一点P"的位置以及C在P处的单位切向量t，输出为C"在P"的延伸方向l以及单位切向量t在P点相对弧长的变化率

具体对于P0"来说，F算子可表示为：

3.2 通过多点平均提高位置、方向计算精度

为提高P1"与t1的计算精度，可采用与龙格-库塔法相似的原理，在P0"与P1"之间设置多个中间点，然后对中间点的几何信息进行加权平均以精确预测曲线C"在P0"附近的几何形状。

若需保证P1"与t1具有二阶计算精度，则依据二阶龙格-库塔法在P0"与P1"之间设置一个中间点

基于公式计算具有二阶精度的P1"与t1，得到：

式中：2P1"与2t1的左上标2表示这些变量具有二阶计算精度。

若需保证P1"与t1具有四阶计算精度，则依据经典四阶龙格-库塔法在P0"与P1"之间设置三个中间点它们采用如下公式进行计算：

式中：4P1"与4t1的左上标4—这些变量具有四阶计算精度。

需要注意的是，迭代过程中方程与方程无法保证2t1与4t1为单位向量，这可通过下式进行调整：

在求得P1"的位置以及曲线C在P1处的单位切向量t1后，可以采用与前述相似的步骤求得后续点P2"、P3"…..，直到曲线抵达曲面边界或离散点的数量满足规定要求。

显然，这些离散点[P0"、P1"、P2"......]定义了参数空间中具有规定测地曲率的曲线C"。

为验证所提出方法的有效性，本节将该方法与现有的方法在计算精度以及计算时间方面进行比较。

在接下来部分给出了三个算例。每个算例中采用现有的方法计算参数曲面上一系列具有规定测地曲率的曲线，直到曲线抵达曲面边界。同时，记录计算过程所消耗的时间。

另一方面，以计算曲线末端点与理想曲线末端点在三维空间中的距离Error作为评价计算精度的指标。

显然，Error越小表示方法越精确。由于很难通过解析方法获得一般曲面上理想的具有规定测地曲率的曲线，因此本节中的理想曲线均采用数值解法求得。

为保证理想曲线具有足够高的精度，数值解法采用了RK4数值积分器以及极小的计算步长。

为便于比较计算精度，计算过程中令各方法的计算步长保持恒定。

文中所有的代码均在MATLAB 2016b环境中实现，然后运行于个人电脑[Intel Core™i5-8400，16G]上来测试计算效率。

如图2所示，算例1计算一个2×2B样条曲面上的等测地曲率曲线。

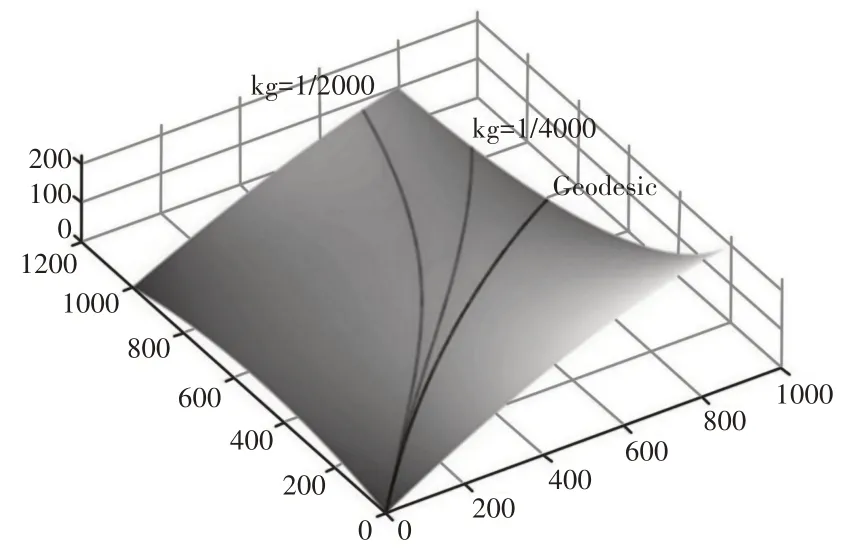
图2 2×2B样条曲面上的等测地曲率曲线Fig.2 Curves with Constant Geodesic Curvature on a 2×2B Spline Surface

计算结果，如图3、图4以及表2所示。

图4 算例1中计算时间对计算精度的影响Fig.4 Influence of Time Costs on Accuracy in Example 1

表2 算例1中各方法所消耗的计算时间Tab.2 Time Costs of Each Method in Example 1

图3 算例1中计算步长对计算精度的影响Fig.3 Influence of Step Size on Accuracy in Example 1

其中，不同方法在相同计算步长下的计算精度以及计算步长对计算精度的影响，如表3所示。

不同方法在相同时间内所能获得的精度，如表4所示。计算过程消耗的时间，如表2所示。

在以下图示中，RK4、RK2表示采用文献[16]中的数值方法以及RK4、RK2数值积分器进行求解，Hu’s表示采用文献[12]中的几何方法进行求解，Zhang’s表示采用文献[11]中的几何方法进行求解，Our4、Our2则表示采用提出的四阶与二阶方法进行求解。

另外，为减小文章篇幅，表2、表3、表4 只列出了部分实验数据。

表4 算例3中各方法所消耗的计算时间Tab.4 Time Costs of Each Method in Example 3

算例2计算一个双三次B样条曲面上的等测地曲率曲线，如图5所示。

图5 双三次B样条曲面上的等测地曲率曲线Fig.5 Curves with Constant Geodesic Curvature on a 3×3B Spline Surface

各方法在相同计算步长下的精度以及计算步长对精度的影响，如图6所示。

图6 算例2中计算步长对计算精度的影响Fig.6 Influence of Step Size on Accuracy in Example 2

它们在相同时间内所能获得的精度，如图7所示。

图7 算例2中计算时间对计算精度的影响Fig.7 Influence of Time Costs on Accuracy in Example 2

计算过程消耗的时间，如表3所示。

表3 算例2中各方法所消耗的计算时间Tab.3 Time Costs of Each Method in Example 2

算例3计算一个6×7B样条曲面上的等测地曲率曲线，如图8所示。

图8 6×7B样条曲面上的等测地曲率曲线Fig.8 Curves with Constant Geodesic Curvature on a 6×7b Spline Surface

计算结果，如图9、图10以及表4所示。

图9 算例3中计算步长对计算精度的影响Fig.9 Influence of Step Size on Accuracy in Example 3

其中，计算精度随步长以及计算时间的变化规律，如图9、图10所示。计算过程消耗的时间，如表4所示。

图10 算例3中计算时间对计算精度的影响Fig.10 Influence of Time Costs on Accuracy in Example 3

由图2、图5、图8可知，测地曲率的幅值决定了曲线偏离测地线的程度，测地曲率的正负决定了曲线所处的方位。

具体地说，当测地曲率为正时，曲线位于测地线延伸方向的左侧；
当测地曲率为负时，曲线位于测地线延伸方向的右侧。

首先，考虑计算精度问题。

由图3、图6、图9可看出，随着计算步长的减小，各方法的计算精度均有所提高。

同时，方法阶数越高，收敛速度越快。对于四阶方法（RK4与Our4），当计算步长很小时，计算结果容易产生震荡，此时继续减小步长对改善计算精度的效果不显著。由计算结果可看出，现有的几何方法精度较差，这主要是由于这些方法无法保证较高的方向计算精度。

对于二阶方法而言，文中提出的方法在精度上要优于文献[16]中的数值解法；
对于四阶方法而言，文中提出的方法在多数情况下可以获得更好的计算精度。

另外，计算结果表明四阶方法的计算精度要显著高于二阶方法，这主要是由于所构造的曲线光滑连续，在解光滑的情况下，高阶方法通常优势明显。其次，考虑计算时间。由表2、表3、表4可看出，随着计算步长的减小，计算过程消耗的时间显著增加。

由上表可看出，与四阶方法相比，现有的几何方法消耗的计算时间更少，这主要是由于这些方法在计算过程中无需进行多点平均、多次迭代。

文献[12]中的几何方法计算速度较慢，这主要是由于该方法在每一步计算中需要进行点到曲面的投射操作。通过比较发现，本方法在时间消耗上与现有的数值方法大致相当。

为综合考虑计算精度与计算时间，图4、图7、图10 展示了不同方法在相同时间内所能获得的计算精度。结果表明，在相同时间内，本方法获得的计算精度一般要优于现有的数值解法，即计算效率更佳。同时，现有的数值方法在计算效率上要优于几何方法。

5.1 自动铺带

自动铺带技术是一种增量制造技术，适用于制造翼面、壁板等大尺寸、小曲率复合材料构件，具有加工成本低、效率高等特点。

在自动铺带工艺中，复合材料预浸带在铺带头的作用下沿着特定轨迹铺贴到模具表面，如图11所示。

图11 自动铺带工艺原理图Fig.11 Sketch of Automated Tape Placement

铺带轨迹需保证单条预浸带不产生过大变形进而发生铺放褶皱，同时需保证相邻两条预浸带满足一定的铺放间隙要求。通常情况下，相邻两条预浸带间不允许产生覆盖，且铺放间隙大小不能超过2.5mm。

现有的商用铺带软件一般基于测地线规划预浸带的铺放路径以保证带料变形最小[19]。

由于模具曲面高斯曲率的影响，相邻两条预浸带间难以保持完全平行，导致铺放间隙问题的产生。

一自由曲面模具，如图12所示。其尺寸为（1000×5000）mm。L1、L2…L7是自由曲面模具0°铺层中所铺放的预浸带。预浸带型号为5228/T700，宽度为150mm。

图12 自由曲面模具上相邻带料间的铺放间隙分布Fig.12 Distribution of Gap on Freeform Mould Surface

为保证带料变形最小，L1、L2…L7的初始铺放路径沿着测地线。由于该自由曲面不可展，相邻测地线间无法保证完全平行，导致铺放间隙问题的产生。如图所示，相邻两条带料L6与L7之间末端的铺放间隙大小接近10mm，这将严重影响最终产品的质量。铺放间隙的大小采用了文献[20]中的方法进行计算。

接下来部分将采用提出的四阶方法构造自由曲面上的等测地曲率曲线，以实现预浸带在模具曲面上的微小转向，消除带料间过大的铺放间隙。

采用等测地曲率曲线的目的在于将整条预浸带需要的转向均匀赋予到轨迹上的每一点，可以防止预浸带在轨迹某一点处出现变形集中进而产生铺放褶皱，从而保证铺带产品的最终质量。

显然，调整后Li的铺放路径应该在调整前Li铺放路径的右侧才能消除Li与Li-1之间过大的铺放间隙，由第四节内容可知，Li的铺放路径上测地曲率符号为负。为获得铺放路径上测地曲率的幅值，可采用折半搜索法，具体，如图13所示。

图13 折半查找流程图Fig.13 Flowchart of the Bi-Section Search

在图13 中，Upper_bound 为折半查找法的上边界，Lower_bound 为折半查找法的下边界，满足|Upper_bound|＞|Lower_bound|，Δ1、Δ2—初始上边界与下边界，它们的数值，如表5所示。

表5 折半查找的初始上边界与下边界Tab.5 The Initial Upper Bound and Lower Bound for the Bisection Search

折半搜索法的停止条件为1.5mm ≤End_Gap≤2.5mm，其中End_Gap表示Li与Li-1之间末端的铺放间隙大小。当折半搜索完成时，Li的铺放路径上测地曲率记为kg（Li）。

折半查找完成后测地曲率及铺放间隙的大小，如表6所示。

表6 折半查找完成后测地曲率及铺放间隙的大小Tab.6 Value of Geodesic Curvature and Gap After the Search Procedure is Finished

调整铺放路径前、后相邻预浸带间铺放间隙的分布情况，如图14所示。

图14 调整铺放路径前、后铺放间隙的分布情况Fig.14 The Distribution of Gap on the Mould Surface

其中一条曲线表示优化前铺放间隙的分布，另一条曲线表示优化后铺放间隙的分布。

由该图可看出，采用本方法所构造出的等测地曲率曲线成功实现了预浸带在模具曲面上的转向，消除了带料间过大的铺放间隙。

优化前后模具曲面上的铺放路径，如图15所示。

图15 优化前后自由曲面模具上的铺放路径Fig.15 The Lay-Up Trajectories on the Freeform Surface

其中，一条曲线表示原始的铺放路径；
另一条曲线表示调整后的铺放路径。

采用第三节中的四阶方法进行轨迹规划时铺放路径L1、L2…L7的计算精度以及7条曲线总的计算时间消耗（未包含折半搜索的时间消耗），如图16所示。

图16 本方法与文献[16]中方法的对比Fig.16 Comparison of Our Method with Reference[16]

由该图可看出，与现有的数值方法相比，本方法在相当的计算时间内可以得到更好的计算精度，即计算效率更高。

具体的说，当计算步长为10与1时，本方法平均计算误差为2.3E-7 与3.47E-11，而文献[16]中的方法平均计算误差为7.3E-7与7.92E-11。

5.2 纤维缠绕

纤维缠绕工艺同样是一种复合材料自动化加工工艺，一般应用于压力管道、压力容器等回转体的制造。

近年来，该工艺也逐渐被应用于制造叶片、飞机S型进气道、三通管等非回转体异型面[21]。

本方法可应用于纤维缠绕工艺中非测地线缠绕轨迹的设计。非测地线缠绕对测地曲率的要求为：缠绕轨迹上各点的测地曲率与轨迹在该点处法曲率的比值不能超过纤维与模具之间的最大静摩擦系数[22]。

现有的研究在处理异型面缠绕时通常基于网格化方法，即先将原始曲面离散为由许多微小面片组成的网格曲面，然后在网格曲面上设计缠绕轨迹。

网格化方法的计算精度与离散网格的精细程度直接相关，当网格划分很精细时，网格曲面的生成需要消耗较多的计算时间。另外，该方法也难以保证设计出的轨迹完全位于原始曲面之上。

本方法不需要生成离散曲面，只要目标曲面能够通过参数方程进行表达，就可以设计出高精度的非测地线缠绕轨迹。

采用本方法设计非测地线缠绕轨迹时，需对F算子中公式进行调整，此时单位切向量t0在P0点相对弧长的变化率需通过下式计算：

式中：λ—纤维缠绕的滑移系数。

图17显示了一个基于自由曲面表达的异型管道，以及采用第三节中四阶方法所设计出的不同滑移系数的非测地线缠绕轨迹，这些轨迹具有很高的计算精度且完全位于目标曲面之上。

图17 异型管道上不同滑移系数的非测地线缠绕轨迹Fig.17 Non-Geodesic Winding Paths on a Non-Revolution Surface

提出了一种参数曲面上具有规定测地曲率曲线的几何方法，当给出目标曲面上的起始点、方向以及测地曲率的分布时，可追踪出符合设计要求的空间曲线。

与现有数值方法相比，本方法无需建立以及求解反映具有规定测地曲率曲线的复杂数学模型，且对于不同的参数曲面具有统一的求解格式；
与现有的几何方法相比，本方法利用多点平均可以得到很高的计算精度。

实验结果表明，本方法在计算效率上要显著高于现有的几何法，且一般情况下要优于数值解法。本方法可应用于自动铺带轨迹规划以及纤维缠绕工艺中非测地线缠绕路径的设计。

为便于比较各方法的计算效率，文中未考虑在计算过程中动态调整计算步长。

如何合理利用每一步计算所得到的几何信息设计变步长方法将是下一步的研究重点。