巧用“反例”培养学生的高等数学逆向思维

史战红，赵有益

(甘肃农业大学 理学院，甘肃 兰州 730070)

在新农科建设的大背景下，高等数学课程对提升农科类院校学生的创新意识、创新能力以及培养学生的抽象能力、思维能力均会起到很大的促进作用。长期以来，高等数学在大学课程体系设置中一直占有着重要的突出地位，作为一门农科类院校开设的公共基础课，该课程的主要目的之一是培养学生具有良好的数学素养和数学思维。在新农科建设的背景下，国家要求农科类院校培养的农业人才要具有较好的创新能力和思维创造性，而高等数学课程对提高大学生的创新能力和思维创造性具有很好的促进作用，这是毋庸置疑的[1]。该课程除了其自身的完整性，往往还是许多专业课的基础，对大学生的后续学习往往会产生深远的影响[2]。通过高等数学课程的学习，不但可以培养学生科学、严谨的思维能力，而且还可以锻造学生的创新精神和实事求是的科学态度。但在实际教学中，我们发现学生对高等数学的学习有时存在恐惧心理，尤其对一些重要定理和结论的理解不够深刻，没有真正理解所学知识的内涵和深层含义，一知半解。为了提高学生的学习兴趣，引导学生对重要结果进行深层次的探究，我们在高等数学教学中，在强化学生常规思维定势能力的基础上，教师有必要刻意地对学生进行一些逆向思维能力的培养[3]。其实逆向思维是创造性思维的另一重要组成部分，在高等数学教学中往往可以出其不意地培养学生的数学思维能力,高等数学学习过程中的逆向思维方法是不能缺少的[4]。高等数学课程中的概念和定理非常多，经过多年的课堂教学，我们发现对农科类学生而言，理解并充分掌握高等数学中的这些概念和定理有点困难。对一些比较抽象的定理和结论，教师如果在课堂上仅仅单纯地从正面讲解、推导和证明，并不能给学生留下比较深刻的印象，有些结论我们需要从反面去论证说明，也就是举反例[5]。在高等数学教学中适时而恰当地举出一些有代表性的反例，不仅有助于培养学生的正向思维能力，而且对学生逆向思维能力的培养和提升也具有非常重要的作用[6]。反例教学往往可以起到事半功倍的效果，从而能够有效地提高高等数学课程的课堂教学质量。比如法国著名数学家费尔玛在1640年前后给出的一个猜想：“对任何非负整数n，形如Fn=22n+1的数都是素数”，对这个命题的正确性，在将近100年的时间内都没有得到证明，直到1732年由瑞士数学家欧拉给出了一个反例：“F5=225+1=641×6700417”，才宣布了费尔玛猜想不成立。再如数学上非常有名的哥德巴赫猜想[7]，从1742年德国数学家哥德巴赫提出该猜想至今，已近300年，但还没有人能够从正面给出严格的证明，同时也没有人能够举出反例说明该猜想不正确。

在信息化高度发达的今天，中国的新农业、新农村、新农民已与互联网、物联网、大数据和区块链等技术紧密地结合到了一起。面对这种新的变化，中国的“三农”问题和乡村振兴战略急需创新型和应用型的新型农业人才，各类农业院校也应审时度势，根据自身的办学特色和学科优势，积极调整，构建新的人才培养模式。在这种新农科建设的背景下，高等数学课程的重要性显得尤为突出，新时代人才必须要有扎实的数学基础和良好的数学思维，同时高等数学课程也肩负着提高学生利用数学知识解决实际问题的水平和培养学生创新能力的重任。目前，高等数学是一门影响很大、授课面也很广的基础理论课，该课程具有其独特的数学理论抽象性及解决问题的技巧性，学生学习的积极性和课堂教学的有效性会直接影响到后续课程的学习[8]。但在平时的课堂教学过程中，我们发现有相当一部分同学对该课程的学习积极性并不是很高，学生在学习过程中也会经常感到高等数学的学习很枯燥，有些结论晦涩难懂。针对这种现象，我们可以在高等数学的课堂教学中适时而恰当地举一些反例，以此来提高学生的学习兴趣，激发学生的学习积极性。经过多年的实践，我们发现如果在高等数学课程的教学过程中适时而巧妙地运用一些反例，学生思考问题的逆向思维能力可以得到有效地提升，同时也能提高课堂教学效果，激发学生的学习积极性。

例1 在无穷小的教学中，我们注意到无穷小有以下两个重要性质：

(1)有限多个无穷小的和还是无穷小；

(2)无穷小与一个有界函数的乘积仍为无穷小。

另外，对性质(2)，如果要说明无穷小换成无穷大后结论不一定成立，即无穷大与有界函数的乘积未必一定是无穷大。我们可举反例：f(x)=x，g(x)=D(x)(其中D(x)为狄利克雷函数)，当x→∞时，虽然f(x)为无穷大、g(x)为有界函数，但f(x)g(x)并不是无穷大。

通过这些简单而易懂的反例，引导学生深入思考课本知识点的本质；
同时，让学生观察和比较初等数学与高等数学的异同点。其实，初等数学很多结论中的常数变成无穷大后结果会发生本质的变化，如以前熟悉的1的任何次幂仍为1，但高等数学中的“第二个重要极限”告诉我们1的无穷大次幂不再是1。这些结果都可以引导学生进一步深入思考和探究其内在原因，让学生切身感受到所学课本知识的趣味性，激发学生学习高等数学的积极性和主动性。

在高等数学的教学中，一些重要的定理和结论往往会让学生感到迷茫和费解，对这些定理的讲解，若考虑反问题(包括条件的充分性和必要性)并对有关结果不成立的情况进行讲解进而举出典型的反例，既有利于加强学生对基础知识的掌握，也可以让学生从另外一个侧面去认识定理的本质，从而理解定理中所给条件的意义。这样既可以帮助学生从不同角度思考和分析问题，也可以培养学生提出问题和分析问题的能力，力争使学生在思考问题时考虑得更加全面。

函数极限的“ε-δ”定义是学生在高等数学中接触的第一个比较枯燥同时也是最难理解的定义，在教学过程中可以给出与该定义相反的叙述：函数f(x)在Uo(x0)内有定义，如果对常数A，存在一个正数ε1，使得对任意的δ>0，存在满足0<|x1-x0|<δ的x1，使不等式|f(x1)-A|>ε1成立，则称函数f(x)在x→x0时的极限不存在。

通过对“ε-δ”定义正面与反面的比较和对照，有助于学生更深层次地理解和认识该定义的内涵。

例3 罗尔中值定理：如果一个函数f(x)满足如下三个条件：(1)[a,b]上连续，(2)(a,b)内可导，(3)f(a)=f(b)；
则至少存在一个点ξ∈(a,b)，有f′(ξ)=0。

高等数学中的微分中值定理部分，对罗尔中值定理的深刻理解有助于学生掌握其他微分中值定理如拉格朗日中值定理、柯西中值定理等，同时也便于学生更好地理解和掌握导数的应用。在该定理的讲解中，为了强调定理的三个条件是结论成立的必不可少的条件，若缺少其中一个条件结论可能会不成立，可以分别举出如下反例：

(2)绝对值函数f(x)=|x|(-1≤x≤1)虽然在[-1,1]上连续，且f(-1)=f(1)，但由于其在开区间(-1,1)内并不可导，从而不存在一个点ξ∈(-1,1)，使f′(ξ)=0成立；

教学中通过列举这些简单直观的反例，让学生感受到定理中所给条件的意义和目的，帮助学生正确理解定理的本质以及定理中所给条件的不可缺少性。

高等数学课程的教学既要求对数学公式和定理的推理论证要严格，同时又要求对课本中数学结论的叙述要简练准确。高等数学教学的主要目的之一是培养大学生数学思维的严谨性，通过高等数学的学习，力争让学生养成认真观察、独立思考、探索研究的良好学习习惯[9]。我们在高等数学教学中合理地运用反例，用实例说明某些性质在不同场合并不一样，让学生观察、比较、探究，促使他们对所学知识深入思考，提示学生不能对某些问题轻易下结论，进而培养学生数学思维的严谨性。

例4 在学完定积分的性质后，高等数学中给出了一个定积分可积的充分条件：如果函数f(x)在闭区间[a,b]上连续，那么f(x)在闭区间[a,b]上一定可积。

对这个结论，反过来是不一定成立的。即若f(x)在区间[a,b]上可积，则f(x)在[a,b]上不一定连续。对此可举如下反例：

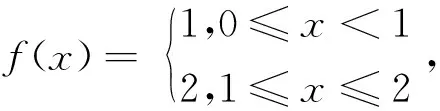
例5 原函数存在定理：若函数f(x)在某一区间I上连续，则f(x)在该区间I上必然存在原函数。但反之不成立，即当f(x)在区间I上存在原函数时，f(x)在区间I上不一定连续。

对此结论，可举反例：

传统观念认为，农科类院校开设高等数学课程的主要目的就是让农学类学生了解一些数学公式和掌握微积分的基本运算。显然，这种观念已不能适应新农科建设的要求，当今社会需要一批创新型人才，我们应该更加注重发挥高等数学课程在提高学生的创新能力和思维能力方面的促进作用[10]。如今的时代是一个创新的时代，在高等数学的教学方法上也必须要有所创新，注重培养学生的创新思维是很有必要的，同时逆向思维是创新思维的重要组成部分，因此课堂教学中巧用反例对提高学生逆向思维能力乃至创新能力的培养有着事半功倍的作用。教学中鼓励让学生自己给一些问题举出反例可以加强学生对基础知识的掌握，通过举反例的方式不但能够培养学生的逆向思维，还可以使学生的创新能力得到更好的训练。

例6 数列极限中有一个定理：如果数列{xn}收敛，则{xn}一定有界。

我们注意到该定理的逆定理不一定成立，对此，可以引导学生举出如下反例：

数列{(-1)n}虽然是有界的，但易见数列{(-1)n}不收敛，是发散的。

例7 定积分中给出了一个可积的必要条件：若一个函数f(x)在闭区间[a,b]上可积，则f(x)在闭区间[a,b]上一定有界。

在教学中，要特别强调该可积的条件是必要而非充分条件。即存在某一函数f(x)在闭区间[a,b]上有界，但f(x)在[a,b]上未必是可积的。对此结论，学生不易理解，可引导学生举如下反例进行说明：

高等数学的课程目标是让学生掌握高等数学的基本概念、理论和方法，即一方面培养学生分析和解决实际问题的思维能力，另一方面培养学生的创新精神和实事求是的科学态度。通过高等数学的学习，让学生建立起比较系统的数学知识体系，具备抽象概括、推理论证、逻辑严密的数学素养。新时代需要的创新型人才必须要有扎实的数学功底，如大数据、人工智能、云计算等现代新技术都要求技术人员要具有良好的数学基础。要让学生很好地掌握高等数学知识，就必须要提高学生的学习兴趣，不能让学生对高等数学课程有惧怕感。近年来，由于农科类院校学生的入校成绩普遍偏低，学生对高等数学的学习兴趣并不是很高，在教学过程中如何提高学生的学习积极性和学习兴趣，一直是我们不断探索和急需破解的问题。经过多年的教学实践，我们发现在高等数学的课堂教学过程中，对抽象和容易产生误解的一些概念和定理进行讲解时，适当而巧妙地选取反例，可以引导学生更深层次地理解和掌握所学概念的本质,同时课堂教学效果也会由于巧用反例而得以提高。不容否认的是，给一个问题举出反例并不是一件很容易的事，在教学中可以采用让学生先自己尝试，然后在教师引导下，鼓励学生边思考边举出反例。通过对某些问题举出反例，不仅可以让学生更深层次地掌握课本中所学的基本概念、基本定理、基本方法，还可以加深学生对知识内涵的理解。总之，在高等数学的教学过程中，教师应积极而主动地尝试多元化的教学形式和教学手段，熟练运用反例，鼓励学生从不同角度思考问题，这不仅可以培养学生的逆向思维，而且可以有效提高学生提出问题、分析问题和解决问题的能力。