求解一类二次规划反问题的同伦交替方向法

高 峰，宇振盛

（上海理工大学 理学院，上海 200093）

反问题研究在投资组合优化和生成树逆问题中具有广泛而极高的应用价值，特别是在网络流逆问题中，为解决信息资源配置问题提供了理论依据和支持。针对反问题，已有大量学者在理论上和算法上进行了深入的研究，并取得了丰硕的成果。早在1996 年，Zhang等[1-2]就已着手研究线性规划反问题，Iyengar等[3]则在2005 年讨论了锥规划反问题。2018 年，Khan等[4]研究了拟变分不等式中参数辨识的反问题，并提出了一种抽象的非光滑正则化方法。具体到二次规划反问题上，Zhang等[5]于2010 年发现此类问题的对偶问题是一个SC1凸问题(即目标函数连续可微并且梯度半光滑)，并且提出使用增广拉格朗日法求解此类问题。针对相同问题，Xiao等[6]于2009 年提出了一种光滑牛顿法进行求解。Lu等[7]在2019 年提出了非凸交替乘子方向法求解一类稀疏的半定逆二次规划问题。李丽丹等[8]在2021 年提出了G-ADMM 法对一类二次规划逆问题进行求解，目标函数是矩阵谱范数与向量无穷范数之和的最小化问题。上述的一些算法虽然全局收敛，但在实际迭代过程中，保证算法线性收敛的前提条件太强而难以满足。除此之外，反问题的目标函数中会出现矩阵范数与向量范数之和，这导致其对偶形式不易求出，因此，就有必要考虑直接对原问题进行求解。为更好解决这类问题，本文使用交替方向乘子法(ADMM)，该方法是解决变量可分离问题的有效方法之一。交替方向乘子法最早由Gabay等[9]在1976 年提出，并且Boyd等[10]在2011年验证了此方法可用来求解大规模的分布式优化问题。同年，文献[11]基于传统交替方向法，在生成迭代步骤的过程中添加了近似二次项，这种方法被称为近端交替方向法(PADM)，但这种近端交替方向法在近端参数的选择上较为敏感。本文提出了一种基于同伦法的ADMM 方法，这种方法将同伦思想融入迭代的每一子问题中，既可克服近端参数选取的敏感性这一缺点，又可加快ADMM收敛速度。

考虑凸二次规划问题QP(G,c,A,b) ：

式中：G∈和c∈Rn分别为矩阵和向量；
为对称半定矩阵集合；
且A∈Rm×n和b∈Rm的值已给定。

传统的正向优化过程是从所有可行解中找到一个最优解x，前提是其中参数G∈，c∈Rn的值会精确给定。但是，反过来讲，有这样一类优化问题，只知道参数G和c的估计值，从经验、观察或者实验中可以知道此问题的可行解，这种情况下，需要找到使给定解成为最优解时的参数G和c的值，并且求得的参数值应该尽可能靠近之前各自的估计值。该类问题称为优化反问题。

反问题在股票市场应用居多，常见的投资组合优化问题可以描述如下：

式中：λ′＞0是控制收益和风险的权重参数；
Ax≤b代表投资组合的约束条件。

一般来说，在一个股票市场里，投资者需要根据目标预期收益来决定每只股票的权重，这就是最优投资组合问题。

而在现实问题中，每只股票的预期收益以及不同股票之间的协方差会随市场的变化而变化。这里用(G0,c0)代表(G,c)的最新估计值，用x0代表问题（2）在(G,c)=(G0,c0)时的最优解。在这种股市变动情况下，投资者先前的投资组合x0不再是新股票市场的最优组合，因为，此时新市场的期望收益变为c0，协方差变为G0，投资者如果继续使用此投资组合将会蒙受经济损失。因此，为了维持经济效益，并且在不改变投资组合的前提下实现原本投资组合x0的价值，需要找出更适用此种投资组合的投资者，而这样的投资者所持股票的期望收益率c和 股票之间协方差G应当尽可能接近第一个投资者股票的期望收益率和协方差的估计值，除此之外，要使得现存投资组合x0为新投资者所持股票组合最优解。因此，找到合适的G和c值极具实际意义。

问题（2）可写成如下的优化反问题：

式中：‖·‖代表矩阵和向量的范数；
ψ(x0)表示x0为问题（2）的最优解时所有(G,c)的集合。

因此，如果(G,c)∈ψ(x0)，即f(G0,c0)=0，那么，此时x0也是问题（3）在参数(G,c)=(G0,c0)时的最优解，这意味着投资者可以继续使用投资组合x0。否则，如果f(G0,c0)＞0，要保证交易成本和回报之间的平衡就要保证估计值(G0,c0)和集合ψ(x0)之间的偏差尽可能小。总之，研究二次规划反问题具有极大的现实意义。

对于问题（1），为方便表示，令

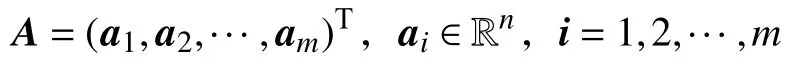
从观测和实验中可以得到参数G和c估 计值G0∈和c0∈Rn，给定一个可行点x0使之满足约束条件Ax0≥b。本文用S(Q)表示Q的最优解，所以，本文研究二次规划反问题的目的即为求出(G,c)∈×Rn的值，使之满足x0∈S(QP(G,c,A,b))，且(G,c)要尽可能接近(G0,c0)。因此，相应的二次规划反问题IQP(G,c)可写为

式中，‖·‖2表示矩阵的谱范数和向量的欧几里得范数，即‖G‖2=max

众所所知，问题QP(G,c)是严格凸二次规划问题，因此，式（4）中的约束，写成KKT条件为[12]

式中，u∈Rm。

不失一般性，假设前p个约束在x0处是有效约束，即x0的积极约束集等价于

令A0:=(a1,a2,···,ap)T,ai∈Rn(i=1,2,···,p)，即A0表示矩阵A的前p行。同时引入向量y，其由向量u的前p个元素构成，所以，x0∈S(QP(G,c))可以等同于

其拉格朗日函数为

交替方向法是求解目标函数可分离优化问题的重要工具。本文为求解一类二次规划反问题，提出了一种基于同伦法的交替方向乘子法，该方法将同伦思想与经典的ADMM 方法相结合。同伦方法最早于1930 年被提出，是解决非线性问题的有力工具，在凸优化和非凸优化方面都做出了巨大贡献。2017 年，Yang等[13]提出了一种基于同伦的交替方向乘子方法来求解线性约束可分离凸极小化问题。本文将同伦方法应用到迭代的每一个子问题上，以此避免敏感近端参数的选取，同时加快了传统ADMM 的速度。

现介绍外迭代使用的近端ADMM 算法以及内迭代使用的逐次超松弛法。

2.1 外迭代

已知(Gk,ck,yk,λk) 的前提下，由ADMM 产生(Gk+1,ck+1,yk+1,λk+1)的迭代结构如下：

（S1）已知(ck,yk,λk)，则有

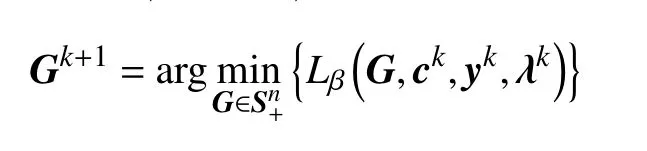
（S2）已知Gk+1，yk和 λk，则有

（S3）已知Gk+1，ck+1和 λk，则有

（S4）拉格朗日乘子 λ的更新为

上述步骤等同于

其中，rk，sk和tk为近端算子。因此，上述迭代过程可重新描述为

实际上，迭代式(7)等同于求解下述方程：

为方便表示，引入符号

综上可知，求解ω*∈W*本质上就是求解非线性方程组F(ω)=0。

定义一个广义同伦映射为[13]

同伦方法是通过选择合适的矩阵H和向量a，再将 αk的值由0 迭代1，得到T(ω,αk)=0的一系列解的过程，特别是，最终αk→1时即可求得F(ω)=0的近似解。总的来说，同伦方法的目的是将求解一个给定的较难问题转化为求解简单问题。原问题F(ω)=0求解起来较为困难，但求解问题(Hωa)=0则相对容易。

现将基于同伦的近端ADMM（HADMM）应用于问题(6)，下面介绍算法。

算法1

2.2 内迭代

现引入逐次超松弛法对上述外迭代过程中的子问题进行内迭代求解。

逐次超松弛法是Gauss-Seidel 法的一种演变方法。它最初是Frankel 在1950 年为了在计算机上求解线性方程而提出的。逐次超松弛迭代法在高斯-赛德尔迭代基础上加入松弛因子以加快迭代收敛速度。

考虑Gauss-Seidel 迭代法

将式（14）中λk+1的更新公式分别与式（15）和式（16）合并，可得

并且，式（14）可重写为

为简单起见，在收敛分析中引入矩阵

其中，Qk=PkMk。令U:=Rn×Rp×Rn，u=(c,y,λ)∈U，已知uk，用uk+1表示由本文算法生成的下一步迭代点。如此便有

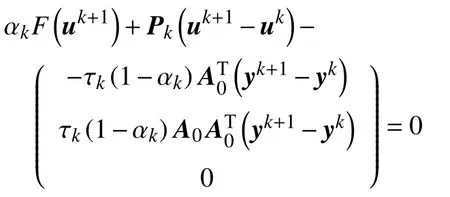
定理1由算法1 生成的序列是收敛的，并且序列极限满足一阶最优性条件式（9）。

定理1 的证明可参考文献[13]，其中也证明了最坏情况下的收敛速度为O(1/k)。

现对本文提出的算法进行数值实验，并与国际知名的优化软件CVX 的子程序SDPT3 和Sedumi求解式（5）的数值结果进行比较。

实验中设置同伦因子初始值，µ及β为

取A，x0和b的值为

并计算出p和A0的值。

参数(G,c,G0,c0)设置为

算法的数值结果如表1 和表2 所示。

表1 HADMM 数值结果Tab.1 Numerical results of HADMM

表1 中，m，n分别表示矩阵或向量的行和列。此处将终止条件设置为ε=10-4。e，t和r分别代表迭代次数，CPU时间和精度。表2 中，字母F 代表计算失败，即迭代次数超过300 次。下标i(i=1,2,3)分别代表HADMM，SDPT3 和Sedumi 这3 个算法。

从表1 和表2 中可以看出，在解决相同维度的问题时，本文的算法无论是在精度还是CPU 时间上，都要优于SDPT3 和Sedumi。除此之外，本文算法能够高效、快速地求解更高维的二次规划反问题。

表2 数值比较Tab.2 Numerical Comparison

采用一种基于同伦的ADMM 方法求解一类二次规划反问题。将该问题转化为目标函数可分离的线性约束问题后，将同伦思想应用于每一次迭代的子问题中，不仅可以实现对传统ADMM 方法的加速，而且避免了选取近端参数时的敏感性。最后给出了算法的数值实验结果。与SDPT3 和Sedumi 的数值结果相比，本文的算法无论是在CPU时间还是残差方面都要优于以上两种方法。最重要的是本文的算法能够更高效求解更高维的问题。