思维中被隐藏的计算——从折纸谈起

陈凯

笔者这样来理解计算思维，它是一种特别的人的思维，这种人的思维可以更具体地认为是一种“能够将机器按机器的方式模拟出某种人的思维”的思维。本文将问题聚焦于这句话中的“人的思维”一词，试着以一些具体的思维活动说明人的思维中本身隐含着计算的思维。这种隐藏着的计算的思维还不能被称为计算思维，直到它被挖掘、显现出来，并向着机器能够运作的方式来进行转化。

● 用折纸来“计算”

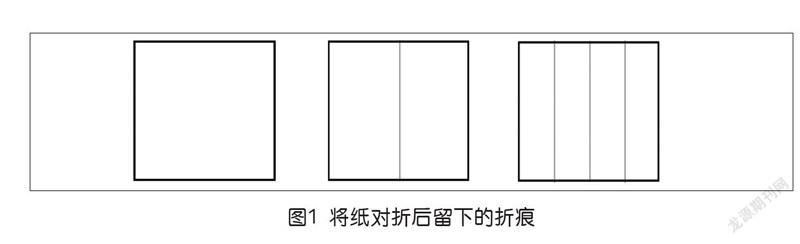
考虑一种简单的依赖折纸来进行“计算”的“装置”，每一张纸都可以对折，从而在纸的中间留下折痕，这样，纸所代表的数字就从1（只有一个区域）变为2（有两个区域），再次对折的话，2就变为4，如图1所示。看上去好像通过不停地将纸对折，就能实现2的n次方的“计算”。

如果同时实施横向和纵向的对折，那么似乎还能让这个“装置”做乘法。例如，为了知道3乘以5的结果是什么，就横向折2次，纵向折3次，这样就显现出4乘8共32个区域。然后标出其中包括了横向3个区域和纵向5个区域的范围，能数出共有15个区域，如图2所示。

可以针对这个例子来提问：这个折纸的过程算不算是一种计算？假设有一台机器，它能接受某个人输入的数值，如3和5，然后就自动开始折纸，最后把3行5列的区域用笔圈出来作为结果还给这个人，那么是不是说这台机器实施并完成了计算？提出这个问题的意图将在后面一起分析。

● 用折好的纸来“计算”

准备好一些对折n次且没有重新摊开的纸，可以想见，对折的次数越多，纸所占的面积就越小，可以从纸的宽窄推测出它所代表的数量，为了方便起见，可以用字母给这些宽窄不同的纸条命名，如图3所示。

接下来是用这些纸条来“计算”3乘以5。找出纸条C和A放在一起代表5，然后将三组C和A的纸条组合排列成3行，如下页图4所示。

接下来，将所有被发现能成对的相同大小的纸条，替换为一张比原有纸条窄一半的纸条，也就是说，两张A型纸条换成1张B型，两张B型纸条换成1张C型，以此类推，直到无可替换为止。最后就能得到用A、B、C、D四种类型纸条组成的序列，代表结果15，如下页图5所示。

重复刚才的问题，如果某个机器可以自动实施这样的操作，算不算是一种计算？

● 8888这个数到底有多大——机器的直观和人的抽象

上面的两个活动，一是用折纸来做3乘以5，二是用折好的纸，并按某种替换规则来做3乘以5，笔者在调查中发现，对于这两种方法，认为其属于计算或不属于计算的，都有不少支持者，有趣的是，认为后一种方法属于计算的人要比认为前一种方法属于计算的人要多。至于为何更多的人认可后者的方法属于计算，解释是多样的。例如有些人说：用前一种方法，就是横向折纸再纵向折纸来做乘法，最终得到的结果不得不需要一个一个去点数，而不是自动给出一个数字;而用后一种方法，最终的结果是以某种符号的形式呈现的，其实对应了二进制数字符号，如当结果是一个A型纸条和一个D型纸条组成的序列，就知道对应的二进制数是1001。

对于这个解释，仔细推敲就可以发现存在说不通的地方，因为即便是面对宽窄不同、用于表达某个数量的纸条序列，若想要知道它所代表的实际数量，就必须把这些折起的纸条摊开，去数一下被折痕所分开的区域总共有多少或者要进一步将不同宽窄纸条所代表的数量进行相加——这似乎让人觉得计算尚未完成。但这个解释提供了一条可以深入思考的线索，那就是人到底是怎样去把握数量的。不妨做一个实验，闭上眼睛，想象一下黑暗的眼前可以同时精确地显现出多少个亮点。例如，笔者自己经过努力，可以在想象的画面中呈现出一个4*4阵列的图案，也就是说，可以同时想象出差不多16个亮点摆放在头脑中。但5*5阵列的图案就很难显现出来，虽然说在想象出来的亮点阵列边缘，每行5个亮点和每列5个亮点仍然很清晰，但整个亮点阵列的图案却是混沌的。即便如此，笔者也能借助深刻脑海的乘法口诀知道那个图案肯定会有25个亮点。不过，如果是一个带传感器的计算机，让它生成或辨识出几百个、几千个、几万个乃至更多亮点，应该都没什么问题。这个例子说明，机器可以直观地去把握数量（这里不讨论机器和人在主动意识上的差异），但人却不行，人只能直观比较少的数量，对于很多数量的东西，只能通过一个抽象的数字系统去记录它。记录和把握其实是两件不同的事，举例说，写下123456789这样的9位数，它很容易记住，但实际上，却不能去直观到这个数量到底有多少。不过，人可以去做抽象的推演，如89其实是8个10加上9，而789其实是7个100加上8个10再加上9。通过这样的方法，人就能确信自己能知道123456789这个数字到底是怎么一回事。假设给出两个数字，一个是十进制数8888，一个是二进制数10001010111000，一般情况下，人自我感觉到仿佛更能够把握前者而不是后者。但无论头脑中出现的是8888这个十进制数字还是它所对应的二进制数字的形式，此人都很难真正用头脑直观地去感知8888个实体的数量，而只是根据日常习惯，下意识地将8888这一系列数字的符号对应为8×1000+8×100+8×10+8的计算规则，因为非常确信这种规则的正确性，以致于不会真的去计算和验证一下。人虽然可以相信8888对应了8888的实际数量，也可以相信10001010111000这个二进制数字也对应了此二进制数字想要表达的实际数量，却不能用直观来确认十进制的8888和二进制的10001010111000这两个数字实质是相等的。这其实说明了，人無法直观一个很大的数量，却能依靠直观来确信自己的数字演算系统是合理的。‬

设想这样一个机器，它能通过传感器数出幕布上亮点的数量，但为了“迁就”人类，就不得不将感知到的数量变成十进制的数码符号呈现出来。人赋予了这个机器抽象的能力，其原因是人自身对数量的直观能力是受限的。但人却有另一种十分重要的直观能力，那就是能将数字演算系统的局部规则的有效性推广到整体，并知道这种推广是正确的，人也相信可以将演算规则推广扩展到机器上，但机器由于自身“禀赋”的限制，其演算过程和人的思维过程可能存在很大的差异。

● ENIAC这样做加法和乘法——人将抽象的过程交予机器模拟

通过古老的ENIAC计算机进行运算的例子，可以进一步说明，有哪些和计算有关的思维被隐藏在一个简单的实现加法或乘法的机械过程中。为简化问题，这里给出了一个极为简化的ENIAC数据存储和显示面板，它由一列数据输入面板和两列数据输出面板组成。表1显示的是用数字7加上数字5这个运算的初始状态。表中的井号表示这里的显示灯亮，也可以认为是此处存储了数字1;格子中如没有井号则表示这里的显示灯不亮，也可以认为是存储了数字0。

操作过程中的每一步动作，会使得当前亮着的灯要么发生变化，要么不发生变化。如果发生变化，则当前格子里的灯会熄灭，而紧邻的上一个格子的灯被点亮，对于最顶端所亮的灯，熄灭后会轮换到本列最底下格子的灯亮起。至于灯什么时候发生变化，则会遵循一系列规则，这个规则和十进制进位法则有关，大家可以观察第93页表2中总共10步动作的情况，然后自己推断灯的变化规律。

需要花费一些时间来理解ENIAC的加法运算过程到底是怎样的。简单地说，无论做什么样的加法，输入端面板的灯必然会跳动10次，可以想见，在运算过程结束时，输入端面板灯的状态就会回到初始时的状态;而只有当输入端面板灯的跳动回转到底部后，输出端面板的灯才会随着输入端面板灯的跳动而一起跳动。ENIAC输入端面板灯必然跳动10次的这个规则其实赋予了它可以进行乘法运算的能力，设想一下，如果输出端面板的数字均为0，输入端只要重复实施加法过程，就能得到乘法运算结果。

对于ENIAC加法过程中灯的跳动方式，观察者能清晰地观察其每一步变化，但调查发现，大部分人无法在一开始就直观地领悟到为什么这种跳动方式是合理的。只有在经过了一些逻辑推理后，才真正领悟到，输入端一开始做的动作，其实是借助10-X的方法获取输入值。举例说，当输入端面板的7号灯被点亮时，机器并不“知晓”这代表了7，当灯向上“爬升”，3次变化动作发生时，输出端都是轮空不动的状态，所以，当灯“触顶”并回转到面板底部时，就剩下了10-3等于7次的数量，可以与输出面板联动进行跳动变化。这种加法过程和人做加法的过程有相当大的不同，人可以通过逻辑推理，确认这个过程实际是对所有的数字普遍有效的。

这里做一个简单的总结，通过折纸和ENIAC实施简单的数学运算的例子，可以发现以下几点：①人在计算过程中，常会用抽象来弥补直观的不足;②人能够直观到抽象的正确性;③人也能够寻找出某种更适合机器实现的机械过程，来代替人的抽象推理过程，并能直观到它的正确性——即便这个过程和人真正的思维过程很不一致。虽然说以上三点都和计算思维有关，但笔者认为，最后一点应该和计算思维有着更密切的联系。回到前文的问题，用折纸或排列折纸序列的方式得到乘法的结果，这是不是一种计算？答案可以是否定的，想象一下，宇宙中存在着许多这种会折纸的某物，但却并不是为了某个特定目的去折纸，同时也没有某种智慧的生物来观察它们的折纸的过程和结果，那么，折纸就仅仅是折纸而已。答案也可以是肯定的，当某种智慧的生物发现纸的状态的变化其实可以对应某种抽象符号系统的变化过程时，折纸也就成为了计算。无论是用折纸来计算，还是用ENIAC来做计算，如果不仅仅看计算结果而是将过程细致地展开，就可知其工作过程和人在做计算时的思维过程有很大的不同，而差異的程度或许可以作为判断完成某项任务中含计算思维“浓度”的一项依据。