基于变分节块法六角形Quasi-diffusion程序开发及验证

庄 坤，王连杰，刘 琨，颜江涛，尚 文

(1.南京航空航天大学 材料科学与技术学院，江苏 南京 211106；
2.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610041)

随着核能的快速发展，基于六角形组件的先进堆型不断涌现，如快中子反应堆[1]、可再生沸水堆[2]、熔盐堆[1]等，与压水堆相比，这些新堆型往往采用更加先进的燃料类型、更加不均匀的燃料布置，其中子能谱与压水堆有很大区别，中子各向异性程度更强，传统轻水堆计算分析方法中的扩散近似假设不再适用。而堆芯燃料管理计算、中子动力学计算是先进堆中子学设计过程中重要的内容，在先进堆的设计阶段，需要反复大量的计算堆芯的功率分布等参数。如果利用中子输运理论，虽然能获得较好的结果但计算效率较低，如果采用传统的扩散理论，虽然可提高计算效率，但堆芯中复杂的中子能谱和强的中子各向异性等特性使得扩散计算的精度较低。因此有必要研究一种既能满足精度需求，又能满足计算效率的先进堆芯中子学计算方法。

Quasi-diffusion是一种低阶中子输运方程，于1964年首次被提出[3]，其形式与传统中子扩散方程相近，不同的是泄漏项表达方式。传统扩散理论建立的基本假定之一是中子的角通量是关于角度的一阶函数，而Quasi-diffusion方程则不采用这一假设，用一个艾丁顿因子表示中子角通量与角度向量的乘积的积分项。艾丁顿因子使得Quasi-diffusion方程具有一些中子流各向异性的输运特性，这是传统扩散理论中所忽略的，由此也可以推断，Quasi-diffusion方程的解的精度要高于传统扩散方程。近年来，国内外许多学者展开了更深入的研究，并探索其在工程中的应用。2009年，William[4]基于2D Quasi-diffusion方程求解2D笛卡尔几何中非结构网格中的输运问题，并给出了一维几何下的艾丁顿因子解析解。2013年，Aristova、Baydin等[5-6]基于Quasi-diffusion方程求解多群输运问题，并计算了三维六边形组件快中子堆临界参数。2013年，Razvan[7]基于节块法和有限体积方法研究了矩形几何和六角形几何下的2维2群Quasi-diffusion方程的计算方法，并将其应用于高温气冷堆中子通量和keff计算，其中艾丁顿因子的计算通过中子角通量的球谐函数展开进行。2015年，Hall[8]利用修改后的SERPENT程序产生组件均匀化截面和艾丁顿因子，基于节块展开法研究了一维情况下的Quasi-diffusion方程的数值计算方法，并推导了节块不连续因子。2018年，Anistratov等[9]基于间断有限元方法和Quasi-diffusion方程研究了一维平板几何中输运问题求解。2019年，Ghassemi等[10]基于Quasi-diffusion方程研究了2D矩形几何下多群热辐射传输问题求解方法。2019年，Jones等[11]基于局部网格离散化技术提出了一种2DR-z坐标系下采用Quasi-diffusion方程求解稳态非结构网格输运问题。2019年，Xu等[12]基于三维截面和Quasi-diffusion方程对TREAT堆芯进行分析。2019年，Olivier等[13]研究了利用Quasi-diffusion加速SN高阶输运方程的计算方法。

可以看出，目前大多数研究将Quasi-diffusion方程应用于加速中子输运计算，艾丁顿因子通过高阶中子输运方程解进行计算，而将Quasi-diffusion方程作为一种像传统中子扩散方程一样的独立方程应用于反应堆计算中的研究还相对较少，主要原因是目前组件程序还不能提供艾丁顿因子。同时，国内外对艾丁顿因子的计算主要采用近似方法，并针对1D和2D矩形几何开展相关研究，而对三维六角形几何的Quasi-diffusion方程的求解方法研究还有待进一步加强。针对艾丁顿因子计算的非线性特点，本文基于两步法的思想，将艾丁顿因子看作是一个特殊的少群参数，采用中子能谱适应性更好的蒙特卡罗程序SERPENT计算。考虑到变分节块法的优势，利用三维节块内的正交基函数对节块内相关变量进行展开，避免传统横向积分技术在处理六角形Quasi-diffusion方程时横向泄漏产生奇异项[14]。

本文对传统扩散变分节块法进行拓展，开发六角形组件堆芯计算程序VNMQD，并采用3D VVER1000基准题、1D RBWR问题、3D BN600简化模型对程序进行验证。

1.1 Quasi-diffusion方程及边界条件

艾丁顿因子张量E表示如下：

(1)

(2)

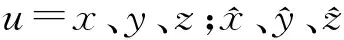
Quasi-diffusion方程中的连续条件是基于中子角通量ψ在两种介质交界面上都是空间r的连续函数得到的，可用下面1组近似条件表示：

(3)

式中：Yn，m(Ω)为球谐函数；
n为展开阶数，m=-n,…,n；
n为交界面法线方向向量；
ψ(r，Ω，E)为r处、Ω方向、能量为E的中子角通量密度。

经过化简即可得到扩散近似方程的连续条件。

流连续边界条件为：

(4)

通量连续条件为：

n·Ex(r,E)φ(r,E)

n·Ey(r,E)φ(r,E)

n·Ez(r,E)φ(r,E)

(5)

式中：J(r，E)为r处能量为E的中子流密度；
φ(r，E)为r处能量为E的中子标通量。

Quasi-diffusion方程中除包含传统的宏观截面(如总截面、裂变截面、散射截面)外，还包含一个重要的量——艾丁顿因子。艾丁顿因子具有以下特点：式(1)中所有元素都在0和1之间，对角元素在1/3附近，非对角元素约等于0，对角元与非对角元有几个数量级的差别。值得指出的是，如果艾丁顿因子在每个区域、每个能群及每个方向上均为1/3，则Quasi-diffusion方程退化为扩散方程，此时意味着中子流是各向同性的。

目前组件程序还不能计算艾丁顿因子，考虑到传统热中子反应堆组件程序在复杂能谱反应堆中应用的限制，以及蒙特卡罗方法具有几何和中子能谱适应性强的特点，本文基于SERPENT进行组件均匀化计算。原版SERPENT不具备艾丁顿因子的计算功能，经过二次开发后可实现艾丁顿因子的计算，并得到了成功的应用[8]。由式(2)可看出，计算艾丁顿因子首先需要知道中子角通量分布，而中子角通量正是需要求解的，因此这是一个非线性问题。通过分析发现，艾丁顿因子与宏观截面具有类似的非线性特点，本文基于两步法的思想，将艾丁顿因子看作是一个特殊的宏观参数，在SERPENT中通过修改其源代码统计每个粒子的飞行方向Ωu、Ωv、Ωw以及沿这个方向的中子角通量变量，并基于式(5)分别计算分子、分母最终得到艾丁顿因子，然后通过并群并区计算得到均匀化区域的少群艾丁顿因子。

由于艾丁顿因子张量对角元与非对角元有几个数量级的差别，本文在实际应用中忽略了非对角元素，因此三维多群Quasi-diffusion方程表示如下：

Σsgφg+Sg

(6)

式中：g为能群编号；
Σtr,g为能群g的输运截面；
φg为中子标通量密度，cm-2·s-1；
Σtg和Σsg分别为中子宏观总截面和群内宏观散射截面，cm-1；
Euug为少群艾丁顿因子；
Sg为中子源项，cm-3·s-1，包括散射源项和裂变源项：

(7)

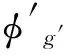
Quasi-diffusion方程中的中子流Jg表达式为：

(8)

式中，Exxg、Eyyg、Ezzg为能群g的艾丁顿因子张量对角线元素。

1.2 六角形几何Quasi-diffusion方程变分节块法求解

本文从三维多群Quasi-diffusion方程出发，利用Galerkin变分和Lagrange乘子法在整个求解域上建立一个包含节块平衡关系和边界条件的泛函，再采用Ritz离散方法将这个泛函进行展开，相应的基函数为空间上的正交多项式函数，得到耦合节块体内的中子通量密度和节块边界上的分中子流密度的节块响应矩阵，最后通过迭代计算实现对方程的数值求解。

根据Galerkin变分原理，Quasi-diffusion方程可在由若干节块组成的整个求解域及其边界上建立全局泛函F：

(9)

式中，节块v的贡献为：

(10)

式中：dv表示对节块v的空间积分；
γ为边界面；
χγg为节块边界上的净中子流密度。

对式(10)中的中子标通量密度φg、中子源项Sg和节块边界上的净中子流密度χg分别利用六角形节块内的正交基函数进行如下展开，为简化省去了能群编号g。

(11)

式中，空间基函数fi、hkγ为完全的正交多项式：

(12)

式中，δij为克罗内克符号。

将式(11)代入式(10)可得到节块泛函与中子通量密度、中子源和净中子流密度的展开系数的关系。

Fv[φ,χ]=φTAφ-2φTs+2φTMχ

(13)

式中：φ、s和χ为中子通量密度、中子源和净中子流密度的展开系数组成的向量；
A和M为矩阵，其计算公式为：

Aij=Pij+δijVvΣr

M=[M1,M2,M3,…]

(14)

随后采用与文献[14]相同的处理方式可得到节块分中子流J+和J-、节块平均中子通量密度φ之间的响应关系：

J+=Bs+RJ-

φ=Hs-C(J+-J-)

(15)

式中，B、R、H、C为几何与材料共同决定的响应矩阵。

式(15)表示六角形节块之间是通过表面的分中子流耦合的，在Quasi-diffusion方程处理时应充分考虑式(4)和(5)的连续性条件。在如图1所示的六角形节块中，对于垂直于坐标轴的面1、面2，其法线方向的净中子流密度由式(16)表示，对于非垂直于坐标轴的面3、4、5、6，其法线方向的净中子流密度由式(17)表示，相应的通量密度连续性条件如(18)、(19)所示。

(16)

(17)

(18)

(19)

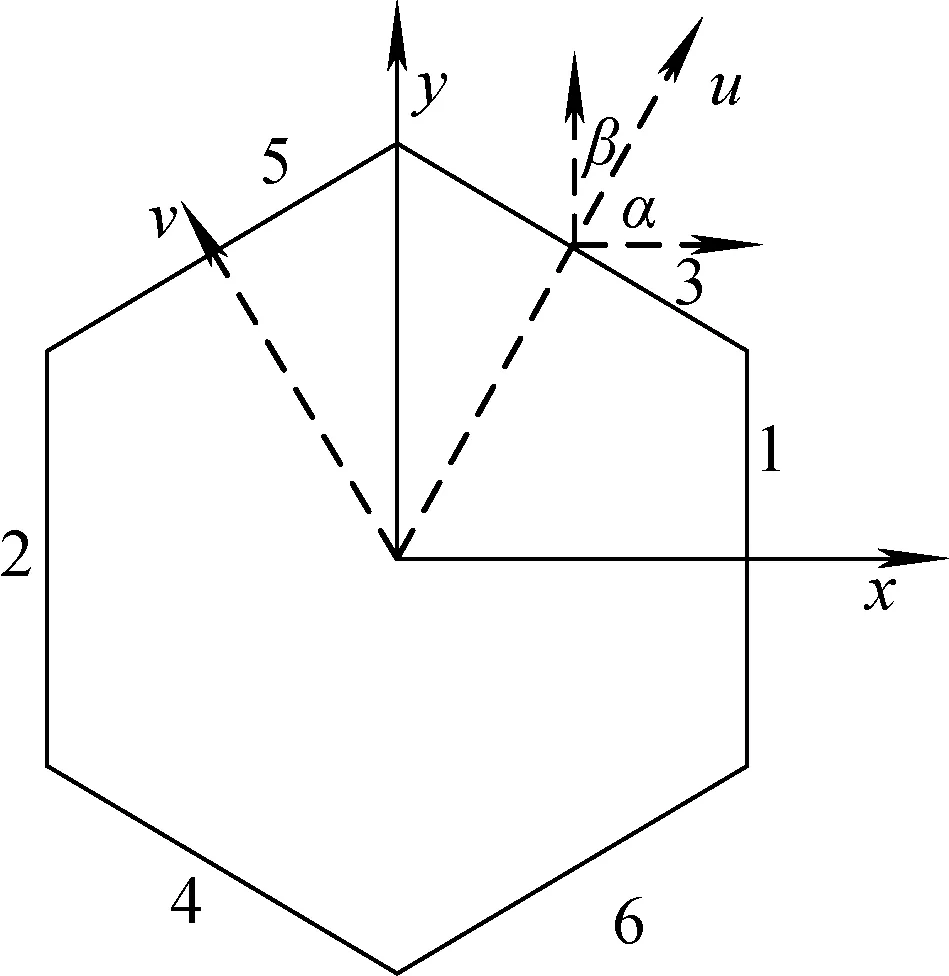
图1 六角形节块示意图Fig.1 Scheme of hexagonal nodal

通过式(18)、(19)及分中子流与净中子流的关系，很容易得到相邻节块在交界面处分中子流的修正表达式：

(20)

fu=Exx对于1,2面

fu=Exxcos2α+Eyycos2β

对于 3, 4, 5, 6面

所有节块通过式(15)耦合，通过红黑扫描策略基于传统的源迭代方法可对整个系统进行求解计算。基于上述理论模型，本文采用FORTRAN90语言开发了六角形变分节块法Quasi-diffusion程序VNMQD，程序计算流程如图2所示。随后采用六角形纯扩散基准题如2D/3D VVER系列问题对VNMQD进行验证，由于该问题为宏观问题，在VNMQD进行计算时设置艾丁顿因子Exx=Eyy=Ezz=1/3。

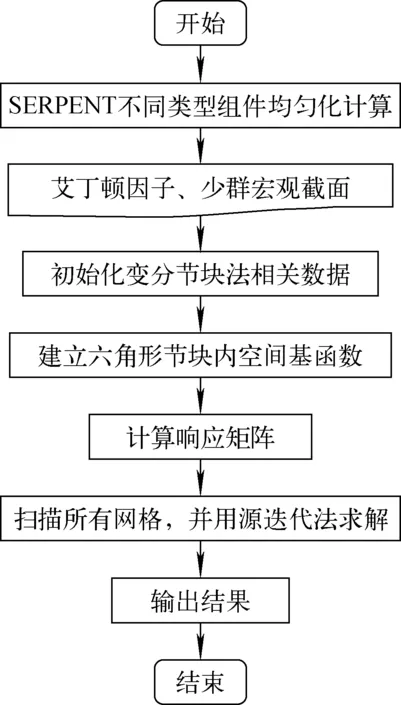
图2 计算流程图Fig.2 Flowchart of calculation

为简化篇幅，本文只给出不带反射层3D VVER1000基准题计算结果。该基准题堆芯轴向高度为200 cm，包含8圈燃料组件(其中包括25根控制棒)，呈1/6旋转对称，径向和轴向反照率分别为0.125、0.15，组件对边距为23.6 cm。VNMQD计算时轴向高度划分为10 cm 1个网格，详细的基准题几何及宏观截面数据参考文献[15-16]。VNMQD计算的功率分布及堆芯有效增殖因数与参考解的比较如图3、表1所示，其中参考解取自文献[15]，对比结果均来自扩散，计算采用0阶散射截面。对比结果可以发现，VNMQD组件功率计算结果与参考解吻合较好，最大相对功率偏差出现在最外层组件为0.3%；
VNMQD计算的keff与参考解符合很好，误差为-11 pcm，且与国际上同类扩散程序AFEN、ANC-H、GTDIF-H、NLSANM具有相同的计算精度。当艾丁顿因子为1/3，Quasi-diffusion方程退化为扩散理论，该系列基准题验证表明VNMQD程序在艾丁顿因子为1/3时编写正确。

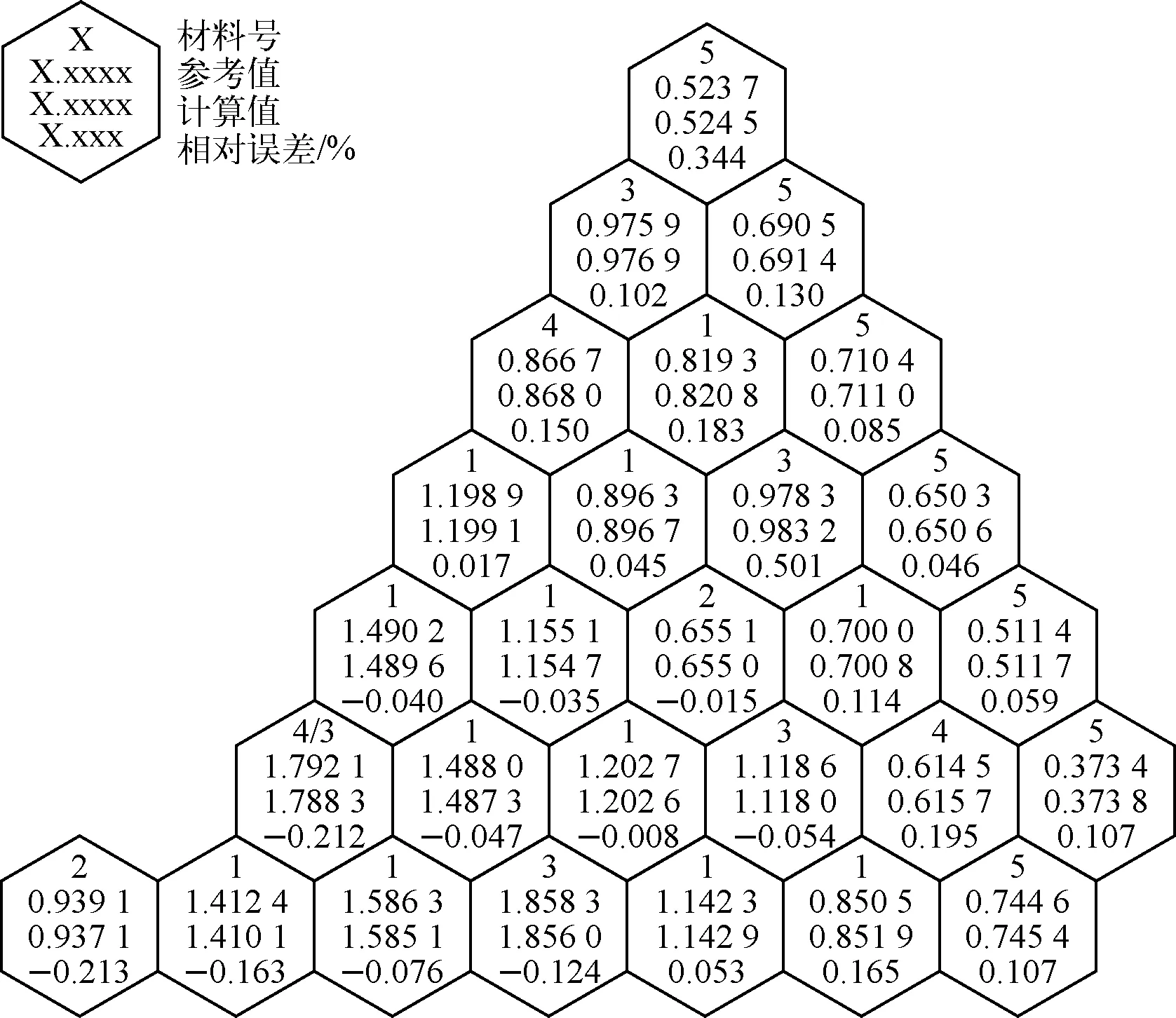
图3 VVER1000基准题组件归一化功率分布Fig.3 Assembly normalized power distribution of VVER1000 benchmark

表1 VVER1000基准题有效增殖因数Table 1 Effective multiplication factor of VVER1000 benchmark

为进一步验证VNMQD的正确性，本文设计了一个1D RBWR单组件问题和3D BN600简化堆芯问题。为尽可能避免由于均匀化模型带来的均匀化误差，特别是艾丁顿因子的均匀化误差，本文采用了全堆芯计算的均匀化模型获得相关均匀化截面及艾丁顿因子。实际上，选取合理的均匀化模型、边界条件等可以避免全堆芯均匀化模型的使用，以增加实用，在这里不作讨论。RBWR单组件问题来源于日本可再生沸水堆设计，该问题具有较强的非均匀性[17]，相关设计参数及材料组成参考文献[8]，如图4所示，外边为全反射边界。由于SERPENT自身画图原因，图4描述的是基于无限组件排布的单组件矩形图。该问题中组件对边距为19.766 8 cm，径向全反射轴向为真空边界条件，轴向高度为134.3 cm，VNMQD在计算中将轴向从下到上分为34层，高度分别为5×5.6 cm、8×2.412 5 cm、8×6.5 cm、8×3.5 cm、5×1.4 cm。采用SERPENT产生12群少群均匀化截面及艾丁顿因子，能群划分列于表2。每层网格产生1套均匀化参数，即34种均匀化截面，VNMQD计算采用0阶散射截面，并对总截面进行1阶散射修正。SERPENT的非均匀计算结果作为参考解，对比包括堆芯有效增殖因数和节块平均中子通量密度。

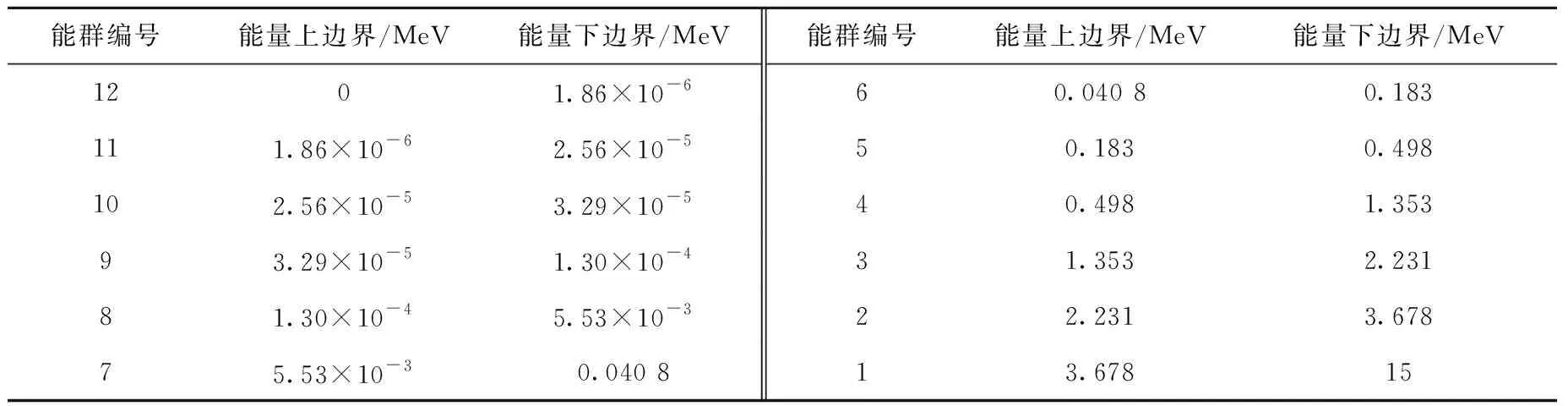
表2 RBWR问题12群能群结构Table 2 Energy structure of 12 energy groups for RBWR benchmark

1D RBWR问题的VNMQD计算结果列于表3，其中no edd情况表示为在计算中艾丁顿因子为1/3，即转化为标准中子扩散计算，其他少群截面则与edd情况保持一致。由表3可见，相比于VNMQD(no edd)，VNMQD(edd)计算的堆芯keff与参考误差更小，为-73 pcm，而VNMQD(no edd)误差达到了-1 738 pcm，两者计算时间相当，约为6.2 s。同样对比了各节块中子通量密度分布及误差，由于趋势类似，本文只给出第1、4群的对比，如图5所示。由图5可见，VNMQD(edd)计算结果与参考值符合更好，第1、4群中子通量密度最大相对误差不超过10%，而VNMQD(no edd)结果最大相对误差可以达到160%。

表3 RBWR问题真空边界条件下VNMQD计算的keff对比Table 3 keff comparison of RBWR benchmark under axial vaccum condition

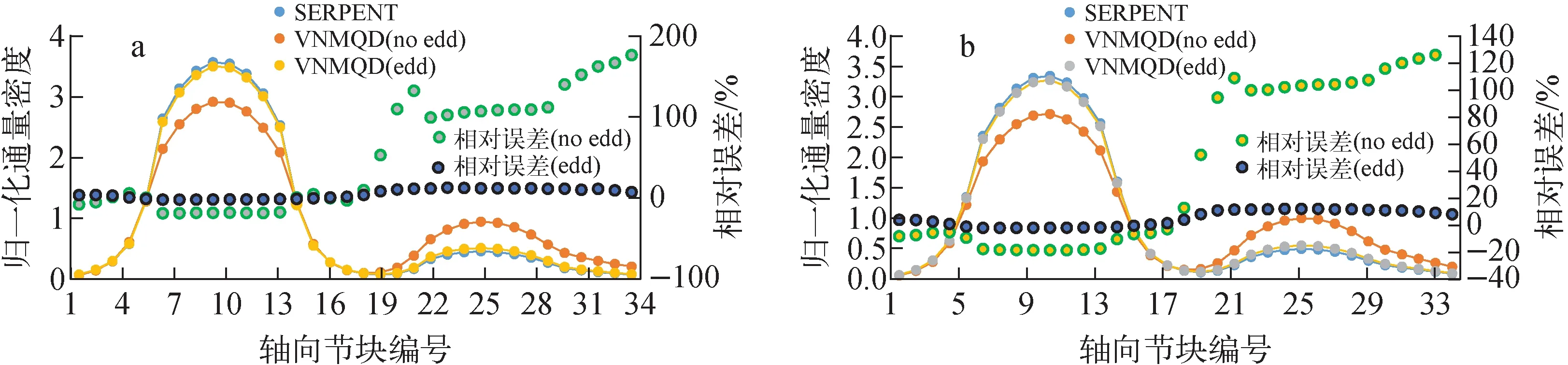
a——第1群；
b——第4群图5 RBWR问题节块中子通量密度对比Fig.5 Comparison of nodal neutron flux density for RBWR benchmark

为验证VNMQD在中子各向异性较强的六角形堆芯中的应用，本文基于BN600快堆基准题[18]中的燃料组件(LEZ、HEZ)和控制组件(SHR、SCR)建立了一个简化的具有12圈燃料构成的堆芯模型，如图6所示，其中组件内的相关材料进行了体积权重打混处理，轴向分层与基准题所述一致，轴向及径向为真空边界条件。采用SERPENT进行精细建模，基于11少群能群结构产生每个节块的均匀化截面及艾丁顿因子，VNMQD计算时轴向高度从底到顶分别为30、4.5、15、4.5、23、5.3、41.15、5.1、41.15、5.5、29.7、30 cm。

图6 BN600简化模型径向和轴向布置Fig.6 Radial and axial configurations of BN600 simplified model

堆芯keff计算结果列于表4，SERPENT计算结果作为参考解，VNMQD计算采用0阶散射截面，并对总截面进行1阶散射修正。由表4可见，与参考解相比，VNMQD(edd)计算结果要比VNMQD(no edd)误差更小，仅为11 pcm，而VNMQD(no edd)误差可以达到-353 pcm，而两者的计算效率接近，计算时间约为3 s。同样对比了不同方法计算的组件平均中子通量密度，如图7所示。由图7可见，VNMQD(edd)计算结果要比VNMQD(no edd)误差更小，在靠近边界处VNMQD(edd)计算精度更高。

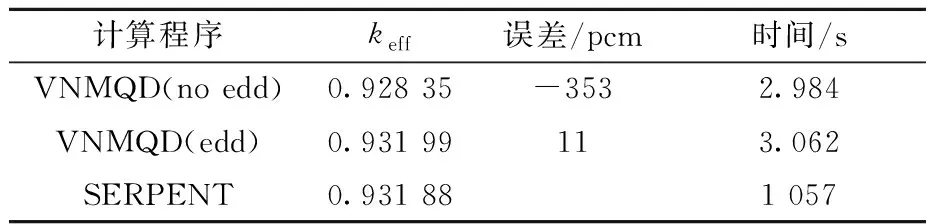
表4 BN600问题真空边界条件下VNMQD计算的keff对比Table 4 keff comparison of VNMQD result for BN600 benchmark at vaccum condition

a——第1群；
b——第4群图7 BN600问题节块中子通量密度对比Fig.7 Comparison of nodal neutron flux density for BN600 benchmark

随着核能技术的快速发展，更加非均匀布置、更强的中子各向异性六角形组件堆型不断涌现，Quasi-diffusion方程比传统扩散方程引入更少的近似，计算精度更高。本文基于两步法的概念，将Quasi-diffusion方程中的艾丁顿因子看作是一个特殊的少群参数，采用几何和中子能谱适应性更好的蒙特卡罗程序SERPENT进行计算，拓展传统扩散变分节块法实现Quasi-diffusion方程的求解，并开发了相应的堆芯中子通量密度计算程序VNMQD。采用基准题3D VVER1000、RBWR单组件、3D BN600简化模型对程序进行了验证，结果表明，VNMQD具有较高的计算精度，对于非均匀性较强的堆芯，Quasi-diffusion比传统扩散在堆芯有效增殖因数和中子通量密度方面计算精度均有巨大提升，而两者的计算效率非常接近。VNMQD开发正确，实现了计算精度和计算效率的平衡。