巧用同构思想妙解一类指对混合压轴题
来源:优秀文章 发布时间:2023-02-15 点击:
福建省永春第一中学 (362601)
刘文哲 张隆亿
对方程或不等式进行变形转化,使其左侧和右侧具有相同的结构形式,再通过构造单调函数处理.对于具有混合指数对数的问题,通常可以通过指数和对数的相互变换实现局部同构.问题可以转化为相应函数单调性或函数最值,这大大降低了计算和求解(证明)的难度.它是数学核心素养如逻辑推理和数学建模的有效媒介,受到高考命题者的青睐.本文提出了指数与对数等式(不等式)的同构方法,并对含指数对数压轴问题的同构解法进行了梳理.
1 利用x=lnex,x=elnx(x>0)进行幂指、幂对转换同构
2 对等式、不等式两边取指数、对数进行同构
2.1 积型aea 1 命题手法1:运用同构思想,转化为h(m(x))形式的式子. 对函数式同构转化,根据结构特点,构造一个对应的函数y=h(x),将涉及函数式h(m(x))问题,转化为这两个函数y=h(x),y=m(x)的最值,达到简化难度的目的.这类试题通常以参数范围和不等式证明等形式进行考查. 2 命题手法2:运用同构思想,转化为h(m(x1))=h(n(x2))形式的等式. 对等式两边同构转化,构造函数y=h(x),等式可以转化为h(m(x1))=h(n(x2)).若函数y=h(x)是单调的,等式可简化为m(x1)=n(x2),从而简化等式,化繁为简.试题常以化简求值,变量的最值等形式进行考查. 例2 (2021孝感期末)若x0为函数f(x)=e2lnx+x-2+lnx-2的一个零点,则e2-x0+lnx0的值为. 解析:根据题意,令f(x)=0,得e2lnx+x-2=2-lnx,两边取对数可得2lnx+x-2=ln(2-lnx),即lnx+x-(2-lnx)=ln(2-lnx),得到lnx+x=ln(2-lnx)+(2-lnx),设h(x)=x+lnx,x∈(0,+∞),则h(x)=h(2-lnx).结合h(x)的单调性可得x=2-lnx,由函数零点的定义可得x0=2-lnx0,所以e2-x0+lnx0=elnx0=x0+2-x0=2. 3 命题手法3:运用同构思想,转化为含有h(m(x1))及h(n(x2))的不等式 对不等式的两边进行同构变换,构造一个对应的函数y=h(x),将原不等式可以转化为含有h(m(x1))及h(n(x2))的不等式,以达到简化不等式结构的目的.试题通常以不等式证明和参数范围等形式进行考查. 3.1 若函数y=h(x)是单调的,则不等式h(m(x1)) 例4 (2020山东21节选)若aex-1-lnx+lna≥1,试求实数a的范围. 解析:将aex-1进行同构变形为ex-1+lna,则不等式aex-1-lnx+lna≥1可整理为ex-1+lna+lna-1≥lnx,两边同加x可得ex-1+lna+lna+x-1≥lnx+x,即ex-1+lna+lna+x-1≥lnx+x=elnx+lnx.令h(x)=ex+x,则h(x-1+lna)≥h(x),可由函数h(x)单调性,得x-1+lna≥x,即lna≥lnx-x+1.利用导数工具可得函数y=lnx-x+1的最大值为0,所以a的取值范围为[1,+∞). 例5 若函数f(x)=lnx-x+1,函数g(x)=axex-4x,a>0,证明:g(x)-2f(x)≥2(lna-ln2). 解析:由axex=ex+lnx+lna可知要证的不等式axex-2x-2lnx-2lna≥2-2ln2可化为ex+lnx+lna-2(x+lnx+lna)≥eln2-2ln2.设h(x)=ex-2x,则h(x+lnx+lna)≥h(ln2).该不等式证明等同于证明函数h(x)的最小值h(ln2),利用函数h(x)的单调性加于验证即可. 3.2 结合转化后不等式h(m(x1))+h(n(x2))<0,不等式的证明可h(x)<0推出.含有双元x1、x2不等式证明,可化归为函数y=h(x)的值域求解,达到化繁为简的目的. 3.3 结合m(x1) 例7 (2022泉州质检二)已知函数f(x)=ax-ex,∀x∈(1,+∞),f(x) 解析1:由alnx+a-ex=a(lnx+1)-elnx+1,得f(x)f(x)对一切x∈(1,+∞)恒成立.结合切线不等式及x∈(1,+∞),得1 简而言之,能直接使用同构的混合指数和对数的导数试题不多.在许多情况下,需要用指数和对数同构技巧,尝试转换为三种常见的同构形式.解决这类含有指数对数导数试题的关键是同构变换,进而构造一个对应函数,将问题转化为函数单调性或函数范围,化难为易,突破解题的障碍点.这类含指数对数压轴题同构解法事实上就是数学建模中建模、解模的过程.在这类导数压轴题求解过程中引入了建模方法,教师应引导学生从不同的角度思考,对同一个问题建立不同的数学解模型,让学生从多个角度学习,寻找不同的问题解决方法,培养创新意识,使他们在面对复杂的函数和导数问题时能够有章可循,一方面提高学生的数学建模技能,另一方面使学生养成有意识地运用数学建模思想解决问题的习惯,往往能达到事半功倍的效果.


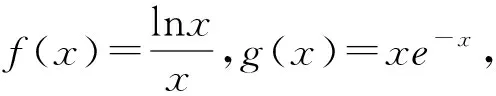
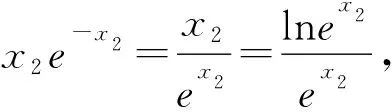
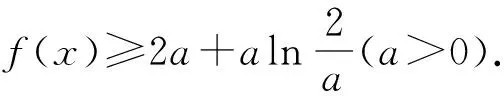


——以指数、对数函数同构问题为例中学教学参考(2022年23期)2022-11-27含有对数非线性项Kirchhoff方程多解的存在性数学物理学报(2022年2期)2022-04-26指数与对数新世纪智能(数学备考)(2021年9期)2021-11-24例谈函数中的同构思想科教导刊·电子版(2021年17期)2021-08-06指对同构法巧妙处理导数题中学生数理化(高中版.高二数学)(2021年2期)2021-03-19同构式——解决ex、ln x混合型试题最高效的工具中学生数理化(高中版.高二数学)(2021年2期)2021-03-19指数与对数新世纪智能(数学备考)(2020年9期)2021-01-04组成等式数学小灵通(1-2年级)(2020年9期)2020-10-27一个连等式与两个不等式链新高考·高一数学(2018年5期)2018-11-22对数简史中学生数理化·高一版(2018年10期)2018-11-08推荐访问:同构
巧用
混合