矩阵方幂的一种简单算法

◎邵逸民

(苏州市职业大学教育与人文学院，江苏 苏州 215104)

定义给定任意一个n阶矩阵A和一个大于1的正整数k，用Ak表示k个A的连乘积，称为A的k次方幂.

对于一些具有特殊结构的矩阵，文[1～3]给出了矩阵方幂计算常用的方法，主要有：

(1)数学归纳法.如果n阶矩阵A的低次幂是有规律可循的.可以先计算A的低次幂，找出其规律，再归纳出Ak并利用数学归纳法证明结论.

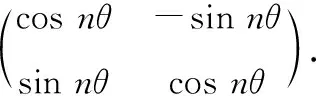
(2)二项式法.如果n阶矩阵A是主对角元素相同的上或下三角阵，则可以将该矩阵写成两个较为简单的矩阵之和从而求出它的方幂.例如，将已知矩阵分解成aE+B(其中E是n阶单位矩阵，B是n阶矩阵)的形式，因为单位矩阵E与矩阵B乘法可交换，所以可用二项式定理进行展开得到结果.

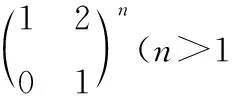
因为B2=0，且E与B矩阵乘法可交换，所以可用二项式定理，故

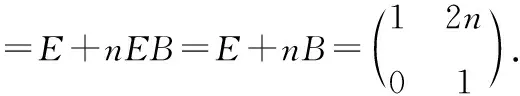
(3)对角化法.当n阶矩阵A可对角化时，可通过求与A相似的对角矩阵B的方幂来求Ak，即如果矩阵A是一个可对角化矩阵，根据相似性，求出可逆矩阵P，使得P-1AP=B为对角矩阵，因为对角矩阵的方幂很容易求出，而BK=P-1AKP，从而AK=PBKP-1，由此即得结果.事实上，实对称矩阵一定可以对角化，故对于实对称矩阵一定可以用这种方法来求.

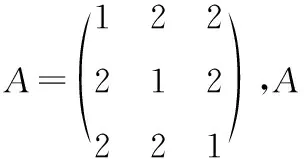
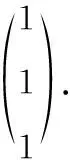
所以A=X[-1,-1,5]X-1,

Ak=X[-1,-1,5]kX-1=X[(-1)k,(-1)k,5k]X-1

(4)Jordan标准型法.若n阶矩阵A的Jordan标准型是矩阵J，可求出可逆矩阵T，使T-1AT=J为Jordan型矩阵.因为Jordan型矩阵的方幂比较容易求出，而Jk=T-1AkT，于是可求出Ak=TJkT-1.因为复数域上任意矩阵都相似于一个Jordan标准型矩阵，Jordan标准型为准对角矩阵，故对于不能对角化的矩阵，可通过求它的Jordan标准型的方幂从而求出矩阵的方幂，因此这种方法具有一般性.但当矩阵的阶数n较大时，求Jordan型矩阵的方幂较为烦琐.

对于λ=1，代数重数是1，在A的Jordan标准形J的对角线上只出现一次，

对于λ=3，因为矩阵A-3E的秩rank(A-3E)=2,从而主对角元为3的Jordan块总数为3-2=1,

下面求出可逆矩阵T，使T-1AT=J为Jordan形矩阵，设T=(X1,X2,X3)，从AT=TJ，得

A(X1,X2,X3)=(X1,3X2,X2+3X3),从而(A-E)X1=0,(A-3E)X2=0,(A-3E)X3=X2,

因为A=TJT-1,所以

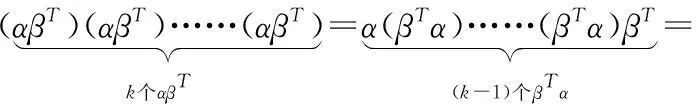
一般来说，当k较大时，矩阵方幂Ak的计算都是复杂的.本文利用矩阵特征多项式和非齐次线性方程组，根据Hamilton-Cayley定理，给出了一种简单可行的解决方法，并通过实例给出了具体的计算方法.为叙述方便，首先给出如下结论作为本文的引理.

引理1[5](带余除法) 对于任意多项式f(x)，g(x)∈P[x]，其中g(x)≠0，一定存在多项式q(x)，r(x)∈P[x]，使得f(x)=q(x)g(x)+r(x)成立，其中∂(r(x))<∂(g(x))或者r(x)=0.

引理2[5](Hamilton-Cayley定理)设A是n阶矩阵，f(λ)=|λE-A|是A的特征多项式，则f(A)=0.

引理3若n阶矩阵A适合一个多项式g(x)，即g(A)=0，则A的特征值λ也必适合等式g(λ)=0.

证明：设α是A的属于特征值λ的特征向量，即Aα=λα，通过矩阵和向量的简单计算，可得g(λ)(α)=g(A)(α)=0，而向量α≠0，因此g(λ)=0.

定理1任何n阶矩阵A的高次幂Ak(整数k≥n)或者等于0，或者可以表示为A的次数不大于n-1的多项式.

证明：设A的特征多项式f(λ)=|λE-A|，用f(λ)去除λk，根据引理1，得λk=f(λ)q(λ)+r(λ)，这里r(λ)=0或r(λ)是次数小于n的多项式.

如果r(λ)=0，则λk=f(λ)q(λ)，由引理2，知Ak=f(A)q(A)=0；
如果r(λ)是次数小于n的多项式，此时，由引理2，知Ak=f(A)q(A)+r(A)=r(A)是A的次数不大于n-1的多项式，定理得证.

根据定理1，若矩阵A不是一个n阶幂零矩阵，则存在r0,r1,…,rn-1，使Ak=r(A)=r0E+r1A+…+rn-1An-1

(1)

于是，由引理，当λ是矩阵A的特征值时，有

λk=r0+r1λ+…+rn-1λn-1

(2)

实际上，(1)式给出了计算矩阵方幂Ak的方法，具体来说，我们有如下定理.

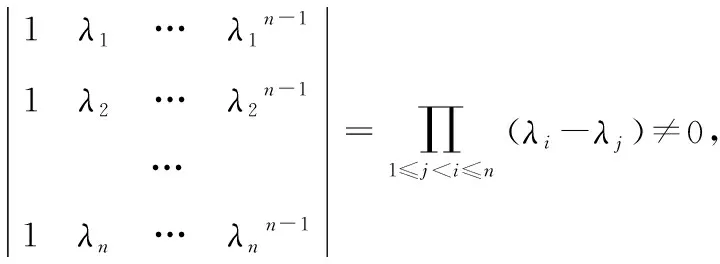
根据定理2，只要知道一个n阶矩阵A的n个不同特征值，就可以由(1)式直接计算出矩阵方幂Ak.定理2的意义主要在于它给出了矩阵方幂与矩阵的特征值之间的明显关系.

需要指出的是，若n阶矩阵A的特征多项式f(λ)=|λE-A|有重根，不妨设λi是它的m重根，则λi也是f(x)，f′(x),…,f(m-1)(x)的根(文[5])，因为λi是矩阵A的特征值，由数学分析中的求导法则可知，只需对r(λ)求导即可，也就是对(2)式两边同时求一阶导数、二阶导数、…、(m-1)阶导数，将λi代入上述等式两边，得到m-1个等式，再与(3)联立方程组，可解出r0,r1,…,rn-1，从而将r0,r1,…,rn-1的值代入(1)式，即可求出矩阵方幂Ak.

1.先给出矩阵特征值互不相同的例子.

令f(λ)=0，求出A的特征值λ1=0和λ2=4.

于是，根据(1)式，计算矩阵方幂，根据定理1和定理2，可得

2.对于矩阵特征值有重根的情形，再给出如下的例子.

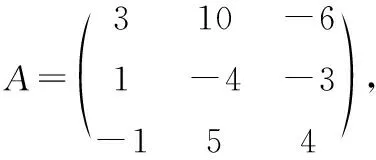
解矩阵A的特征多项式f(λ)=|λE-A|=(λ-1)3=λ3-3λ2+3λ-1，

求出A的特征值λ=1(三重根).

由(2)式，可设λ100=r0+r1λ+r2λ2

(4)

将特征值代入线性方程组(3)，得r0+r1+r2=1100=1

(5)

因为λ=1是A的三重特征根，故分别对(4)式两边求一阶导数和二阶导数，

再将λ=1代入所得两式，有100=r1+2r2

(6)

以及9900=2r2

(7)

联立(5)、(6)、(7)，解得r0=4851，r1=-9800，r2=4950.

于是，(4)式变为λ100=4851-9800λ+4950λ2，根据定理1和定理2，可得

在n阶矩阵方幂的计算中，针对不同结构类型的矩阵，采用适当的计算方法可以化繁为简.通过以上例题的求解，也可以看出用上述介绍的方法计算矩阵的高次幂能有事半功倍的效果.事实上，这种方法同样适用于一般的矩阵多项式计算.